Diffuser In-depth Overview

Introduction to Diffusion Models

Diffusion models have emerged as a powerful new class of generative models in the field of artificial intelligence, revolutionizing the way we create and manipulate visual and audio content. These models have gained significant attention in recent years due to their ability to produce high-quality, diverse outputs that often surpass those of other generative approaches.

At their core, diffusion models are based on a simple yet profound idea: they learn to gradually denoise a signal that has been corrupted with Gaussian noise. This process, inspired by non-equilibrium thermodynamics, allows the model to generate complex data distributions by reversing a diffusion process that gradually adds noise to the data.

The concept of diffusion models was first introduced in the context of machine learning by Sohl-Dickstein et al. in 2015. However, it wasn't until the groundbreaking work of Ho et al. in 2020, introducing Denoising Diffusion Probabilistic Models (DDPMs), that these models began to show their true potential in generating high-quality samples.

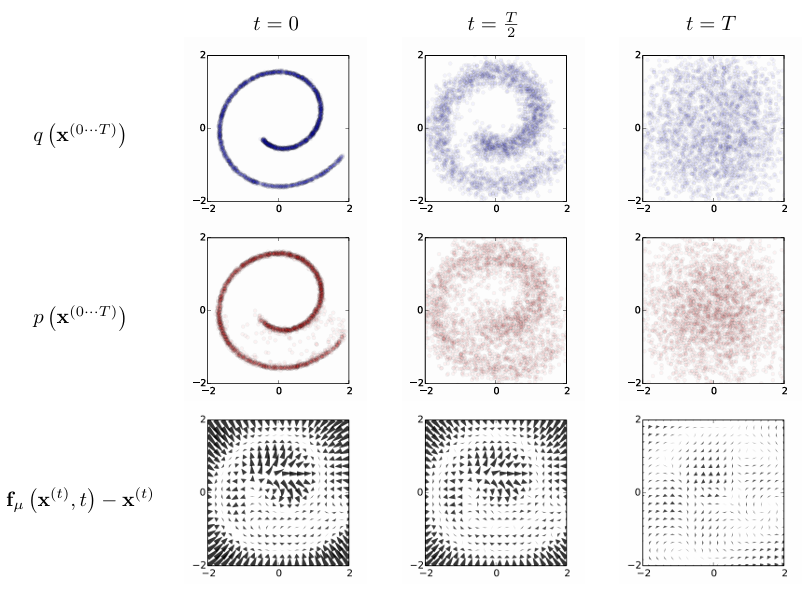
Paper : Deep Unsupervised Learning using Nonequilibrium Thermodynamics

Paper : Denoising Diffusion Probabilistic Models

In the landscape of generative AI, diffusion models occupy a unique position. They offer several advantages over other popular approaches such as Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs). Unlike GANs, which can suffer from training instability and mode collapse, diffusion models are more stable during training and can generate a wider variety of samples. Compared to VAEs, diffusion models typically produce sharper and more detailed outputs.

The impact of diffusion models has been particularly pronounced in the field of image generation. Models like DALL-E 2, Midjourney, and Stable Diffusion have captured public imagination with their ability to create stunning, photorealistic images from text descriptions. These models have not only pushed the boundaries of what's possible in AI-generated art but have also opened up new possibilities in fields such as design, advertising, and entertainment.

Beyond image generation, diffusion models have shown promise in a variety of other domains. They've been applied to tasks such as image inpainting, super-resolution, and even audio synthesis. In the realm of 3D content creation, diffusion models are being explored for generating 3D shapes and textures.

One of the key strengths of diffusion models is their flexibility. They can be easily adapted to conditional generation tasks, allowing for fine-grained control over the generated outputs. This has led to applications such as text-to-image synthesis, where users can generate images based on detailed text descriptions, or style transfer, where the style of one image can be applied to another.

Diffusion models also offer interesting theoretical properties. The gradual denoising process allows for interpretable intermediate steps, providing insights into how the model constructs complex data. This contrasts with many other generative models, which often operate as "black boxes" with less interpretable internal processes.

In terms of training, diffusion models have shown remarkable sample efficiency. They can often achieve high-quality results with less training data compared to some other generative approaches. This is particularly valuable in domains where large datasets are difficult or expensive to obtain.

However, diffusion models are not without challenges. One of the main drawbacks is the computational cost of sampling. The iterative denoising process can be time-consuming, especially for high-resolution outputs. This has led to significant research efforts focused on accelerating the sampling process, with techniques like improved sampling algorithms and architectural optimizations.

As the field of diffusion models continues to evolve, we're seeing exciting developments in areas such as combining diffusion models with other AI techniques, exploring new applications, and improving the efficiency and quality of generation. The rapid progress in this area suggests that diffusion models will likely play an increasingly important role in the future of generative AI, potentially transforming fields ranging from creative arts to scientific research.

In the following sections, we'll delve deeper into how diffusion models work, explore their various applications, and discuss some of the key research directions in this rapidly evolving field.

How Diffusion Models Work

Diffusion models operate on two fundamental processes: the forward diffusion process and the reverse diffusion process. These processes form the core of how diffusion models generate data.

The Forward Diffusion Process

The forward diffusion process is a fixed procedure that gradually adds noise to data. It can be mathematically described as a Markov chain:

$q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)$

Where:

• $x_t$ is the data at step $t$
• $\beta_t$ is the noise schedule
• $\mathcal{N}$ denotes a Gaussian distribution

The complete forward process is expressed as:

$q(x_{1:T} | x_0) = \prod_{t=1}^T q(x_t | x_{t-1})$

This process transforms the original data distribution into a simple Gaussian distribution over $T$ steps.

The Reverse Diffusion Process

The reverse diffusion process aims to invert the forward process. It is learned by training a neural network to predict and remove the noise added during the forward process. The reverse process is described as:

$p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))$

Where $\mu_\theta$ and $\Sigma_\theta$ are learned functions parameterized by a neural network.

The training objective for diffusion models is typically formulated as minimizing the variational lower bound on the log-likelihood:

$\mathcal{L} = \mathbb{E}_{q(x_0)}[-\log p_\theta(x_0)] \leq \mathbb{E}_{q(x_{0:T})}[\log \frac{q(x_{1:T}|x_0)}{p_\theta(x_{0:T})}]$

This can be simplified to a denoising score matching objective:

$\mathcal{L}_\text{simple} = \mathbb{E}_{t,x_0,\epsilon}[||\epsilon - \epsilon_\theta(x_t, t)||^2]$

Comparison to Other Generative Models

Source : Towards AI

Diffusion models differ from GANs and VAEs in several ways:

1. Training Stability: Diffusion models have a more stable training process compared to GANs, which can suffer from training instability.

2. Sample Quality and Diversity: Diffusion models can generate high-quality samples while maintaining diversity, whereas VAEs often face a trade-off between these two aspects.

3. Flexibility: Diffusion models can be adapted to conditional generation tasks by incorporating additional information into the denoising network.

4. Interpretability: The step-by-step nature of diffusion models allows for more interpretable generation compared to single-step models like GANs or VAEs.

5. Mode Coverage: Diffusion models have shown better mode coverage compared to GANs, which can suffer from mode collapse.

6. Computational Cost: The sampling process in diffusion models is typically more computationally expensive than in GANs or VAEs.

7. Sampling Speed: Diffusion models are generally slower at generating samples compared to GANs or VAEs, which can generate samples in a single forward pass.

These characteristics have led to the widespread adoption of diffusion models, particularly in image generation tasks where they have achieved state-of-the-art results. Research continues to focus on improving the efficiency and capabilities of diffusion models.

Key Components of Diffusion Models

Diffusion models have emerged as a powerful class of generative models, capable of producing high-quality samples across various domains. The success of these models relies on several key components that work together to enable the gradual denoising process. Let's explore three critical elements in detail: noise scheduling, U-Net architecture, and loss functions.

Noise Scheduling

Noise scheduling is a crucial aspect of diffusion models that determines how noise is added and removed during the forward and reverse processes. The noise schedule defines the variance of Gaussian noise added at each timestep, controlling the rate at which the data is corrupted or denoised.

The forward process of a diffusion model can be described by the following equation:

$x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon$

where $x_t$ is the noisy image at timestep $t$, $\alpha_t$ is the noise level at timestep $t$, and $\epsilon$ is Gaussian noise.

The noise schedule is typically defined as a function that maps timesteps to noise levels. Common noise schedules include:

1. Linear schedule: $\alpha_t = 1 - \beta t$, where $\beta$ is a constant
2. Cosine schedule: $\alpha_t = \cos^2(\frac{\pi t}{2T})$, where $T$ is the total number of timesteps

The choice of noise schedule can significantly impact the model's performance. Recent research has shown that the optimal noise schedule depends on the task and data characteristics. For instance, when increasing image resolution, the optimal noise schedule tends to shift towards noisier levels due to increased redundancy in pixels.

An effective strategy for adapting noise schedules across different image sizes is to use a fixed noise schedule function (e.g., $\gamma(t) = 1 - t$) and scale the input data by a factor $b$. This approach, equivalent to shifting the log signal-to-noise ratio (SNR) by $\log b$, has shown promising results across various image resolutions.

U-Net Architecture

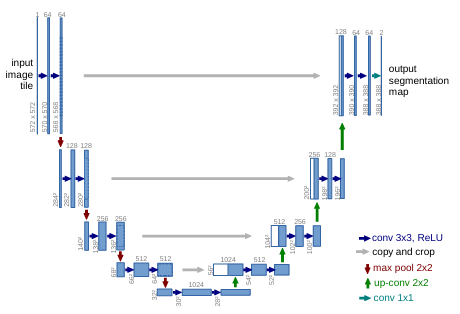
The U-Net architecture is the backbone of many diffusion models, responsible for learning the denoising process. Originally developed for biomedical image segmentation, U-Net has been adapted and optimized for diffusion models.

Paper : U-Net

The U-Net consists of several key components:

1. Encoder: A series of convolutional layers that progressively downsample the input, capturing increasingly abstract features.

2. Decoder: A series of upsampling layers that reconstruct the image from the encoded features.

3. Skip connections: Direct connections between corresponding encoder and decoder layers, allowing the model to preserve fine-grained details.

4. Time embedding: A mechanism to inject timestep information into the network, enabling it to adapt its behavior based on the current noise level.

The U-Net's ability to capture multi-scale features makes it particularly well-suited for the denoising task in diffusion models. The architecture can be expressed mathematically as:

$f_\theta(x_t, t) = \text{U-Net}(x_t, \text{emb}(t))$

where $f_\theta$ is the learned denoising function, $x_t$ is the noisy input at timestep $t$, and $\text{emb}(t)$ is the time embedding.

Recent advancements in U-Net architectures for diffusion models include:

1. Attention mechanisms: Incorporating self-attention layers to capture long-range dependencies.
2. Residual connections: Adding residual blocks to improve gradient flow and ease training of deeper networks.
3. Adaptive group normalization: Using adaptive normalization techniques to better handle different noise levels.

Loss Functions

The choice of loss function is critical in training diffusion models effectively. The most common loss function used in diffusion models is the simplified variational lower bound (VLB) loss, which can be expressed as:

$L_\text{VLB} = \mathbb{E}_{t, x_0, \epsilon} \left[ \frac{1}{2\sigma_t^2} \|\epsilon - \epsilon_\theta(x_t, t)\|^2 \right]$

where $\epsilon_\theta$ is the model's prediction of the noise, $x_t$ is the noisy input at timestep $t$, and $\sigma_t^2$ is the variance of the noise at timestep $t$.

Paper : VLB

This loss function encourages the model to predict the noise added during the forward process accurately. However, researchers have proposed several variations and improvements to the basic VLB loss:

1. Weighted loss: Applying different weights to different timesteps to balance the importance of early and late denoising steps.

2. Hybrid objectives: Combining the VLB loss with other objectives, such as perceptual losses or adversarial losses, to improve sample quality.

3. Learned variance: Instead of using a fixed variance schedule, some approaches learn the variance as part of the model.

The loss function can also be formulated in terms of predicting the clean data $x_0$ instead of the noise $\epsilon$:

$L_{x_0} = \mathbb{E}_{t, x_0, \epsilon} \left[ \|x_0 - x_\theta(x_t, t)\|^2 \right]$

where $x_\theta$ is the model's prediction of the clean data.

Recent work has shown that the choice between predicting noise ($\epsilon$) or clean data ($x_0$) can affect the model's performance, with some tasks benefiting more from one formulation over the other.

In conclusion, the interplay between noise scheduling, U-Net architecture, and loss functions forms the foundation of diffusion models. Ongoing research continues to refine these components, pushing the boundaries of what's possible with this powerful class of generative models. As the field evolves, we can expect further innovations in each of these areas, leading to even more impressive results across a wide range of applications.

Types of Diffusion Models

Diffusion models have emerged as a powerful class of generative models, capable of producing high-quality samples across various domains. Let's explore three important types of diffusion models: Denoising Diffusion Probabilistic Models (DDPM), Latent Diffusion Models, and Stable Diffusion.

Denoising Diffusion Probabilistic Models (DDPM)

Denoising Diffusion Probabilistic Models, introduced by Ho et al. in 2020, form the foundation of modern diffusion models. DDPMs are based on a forward process that gradually adds Gaussian noise to data, and a reverse process that learns to denoise the data.

The forward process is defined as a Markov chain that progressively adds noise to an image over T timesteps:

$q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)$

where $\beta_t$ is the noise schedule.

The reverse process aims to learn the conditional probability $p_\theta(x_{t-1} | x_t)$, which is approximated by a neural network. The objective is to minimize the variational lower bound:

$L = \mathbb{E}_{q(x_0, x_1, ..., x_T)} \left[ \log p(x_T) + \sum_{t > 1} \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} \right]$

DDPMs have shown impressive results in image generation, achieving high-quality samples and diversity. However, they suffer from slow sampling speeds due to the large number of denoising steps required.

Latent Diffusion Models

Latent Diffusion Models (LDMs), proposed by Rombach et al., address the computational challenges of pixel-space diffusion models by operating in a lower-dimensional latent space. LDMs consist of two main components:

1. A perceptual compression model (e.g., autoencoder) that maps between pixel space and latent space.
2. A diffusion model that operates in the latent space.

The perceptual compression model is typically an autoencoder with an encoder $\mathcal{E}$ and a decoder $\mathcal{D}$. The latent representation $z = \mathcal{E}(x)$ is obtained by encoding the input image $x$. The diffusion process then operates on this latent representation.

The objective function for LDMs can be expressed as:

$L_{LDM} = \mathbb{E}_{x, \epsilon \sim \mathcal{N}(0,1), t} \left[ \| \epsilon - \epsilon_\theta(z_t, t) \|_2^2 \right]$

where $z_t$ is the noisy latent at timestep $t$, and $\epsilon_\theta$ is the noise prediction network.

LDMs offer several advantages:

1. Reduced computational complexity due to operating in a lower-dimensional space.
2. Ability to leverage pretrained perceptual compression models.
3. Flexibility in incorporating various conditioning mechanisms.

Stable Diffusion

Stable Diffusion, developed by Stability AI, is a specific implementation of Latent Diffusion Models that has gained significant popularity due to its ability to generate high-quality images from text descriptions. It builds upon the LDM framework with several key enhancements:

1. Improved Autoencoder: Stable Diffusion uses a more advanced autoencoder architecture, allowing for better compression and reconstruction of images.

2. Text Conditioning: It incorporates a powerful text encoder (often based on CLIP) to enable text-to-image generation.

3. Efficient U-Net: The core diffusion model uses an optimized U-Net architecture for faster and more stable training.

4. Advanced Sampling Techniques: Stable Diffusion implements various sampling methods, such as PLMS (Pseudo Linear Multistep) and DDIM (Denoising Diffusion Implicit Models), for faster inference.

The text-to-image generation process in Stable Diffusion can be summarized as follows:

1. Encode the input text using a text encoder.
2. Generate a random latent vector and progressively denoise it using the U-Net conditioned on the text embedding.
3. Decode the final latent representation to produce the output image.

Stable Diffusion has demonstrated remarkable capabilities in generating diverse and high-quality images from text prompts, making it a popular choice for various creative applications.

Applications of Diffusion Models

Diffusion models have revolutionized the field of generative AI, finding applications across a wide range of image-related tasks. Their versatility and high-quality outputs have made them increasingly popular for both research and practical applications.

Image Generation

One of the primary applications of diffusion models is in unconditional image generation. These models have demonstrated the ability to produce highly realistic and diverse images across various domains, from natural scenes to abstract art. The quality of generated images often rivals or surpasses that of other generative approaches like GANs.

Diffusion models excel at capturing fine details and textures, making them particularly effective for generating complex scenes. They can produce images with consistent global structure while maintaining local coherence, a challenging task for many other generative models. This capability has led to their use in creating synthetic datasets for training other AI models, as well as in creative applications for digital art and design.

One of the key advantages of diffusion models in image generation is their mode-covering behavior. Unlike GANs, which can suffer from mode collapse (generating a limited variety of samples), diffusion models tend to produce a wider range of diverse outputs. This makes them valuable for applications requiring a broad spectrum of generated content.

Text-to-Image Synthesis

Text-to-image synthesis has emerged as one of the most impactful applications of diffusion models. By conditioning the diffusion process on textual descriptions, these models can generate images that closely match given prompts. This has opened up new possibilities for creative expression and visual content creation.

Models like DALL-E 2, Midjourney, and Stable Diffusion have captured public imagination with their ability to transform text prompts into striking visual representations. These systems can generate images ranging from photorealistic scenes to stylized illustrations, all guided by natural language descriptions.

The flexibility of text-to-image diffusion models allows for fine-grained control over generated content. Users can specify details about composition, style, lighting, and more through carefully crafted prompts. This level of control has made these models valuable tools for conceptual artists, designers, and content creators across various industries.

Text-to-image synthesis has also found applications in prototyping and ideation processes. Designers and product developers can quickly visualize concepts by generating images based on textual descriptions, streamlining the creative process and facilitating communication of ideas.

Image Inpainting and Editing

Diffusion models have proven to be highly effective for image inpainting and editing tasks. Their ability to understand and generate coherent image structures makes them well-suited for filling in missing or corrupted parts of images.

In image inpainting, diffusion models can seamlessly reconstruct missing regions of an image while maintaining consistency with the surrounding context. This has applications in photo restoration, removing unwanted objects from images, and repairing damaged visual content.

For image editing, diffusion models offer a powerful toolset for making controlled modifications to existing images. By conditioning the diffusion process on both the original image and desired edits (often specified through text prompts or masks), these models can perform complex transformations while preserving the overall structure and style of the original image.

Some specific editing applications include:

• Style transfer: Applying the style of one image to another while maintaining content integrity.
• Object replacement or addition: Seamlessly inserting new objects into existing scenes or replacing elements within an image.
• Attribute manipulation: Modifying specific attributes of objects or scenes, such as changing the season in a landscape image.

The non-destructive nature of diffusion-based editing allows for iterative refinement and exploration of creative possibilities. This has made diffusion models increasingly popular in professional image editing workflows, complementing traditional tools with AI-powered capabilities.

Fine-tuning Diffusion Models

Fine-tuning diffusion models has become an important area of research and practice, allowing these powerful generative models to be adapted for specific domains or tasks. This process involves taking a pre-trained diffusion model and further training it on a new dataset or with additional conditioning information.

Transfer Learning Techniques

Transfer learning in the context of diffusion models leverages the knowledge captured by a model trained on a large, diverse dataset to improve performance on more specific tasks or domains. Several techniques have been developed to facilitate effective fine-tuning:

1. Partial Fine-tuning: Instead of updating all model parameters, this approach focuses on fine-tuning specific components of the model. For example, only adjusting the attention layers or the final few blocks of the U-Net architecture. This can help preserve general knowledge while adapting to new domains.

2. Low-Rank Adaptation (LoRA): This technique involves adding small, trainable matrices to the attention layers of the model. LoRA allows for efficient fine-tuning with a small number of additional parameters, reducing memory requirements and training time.

3. Textual Inversion: For text-to-image models, this method learns new text embeddings for specific concepts or styles without modifying the underlying model architecture. It enables personalization and domain adaptation with minimal computational overhead.

4. Dreambooth: This approach fine-tunes the model to learn a specific subject (e.g., a person or object) from just a few images. It modifies both the text encoder and the diffusion model to create a personalized text-to-image generator.

5. Hypernetworks: These are small neural networks that generate the weights for specific layers of the main diffusion model. Fine-tuning hypernetworks can allow for efficient adaptation without modifying the entire model.

Dataset Considerations

The choice and preparation of the dataset for fine-tuning are crucial factors in the success of the process. Several considerations come into play:

1. Data Quality: High-quality, diverse images are essential for effective fine-tuning. Curating a dataset that represents the target domain or style is critical.

2. Dataset Size: While diffusion models can benefit from large datasets, fine-tuning can often be effective with relatively small datasets (hundreds to thousands of images) when using appropriate techniques.

3. Data Augmentation: Techniques like random cropping, flipping, and color jittering can help increase dataset diversity and prevent overfitting, especially when working with limited data.

4. Balancing: For class-conditional models, ensuring a balanced representation of different classes in the fine-tuning dataset is important to prevent biased generation.

5. Metadata and Captions: For text-to-image models, accurate and descriptive captions or metadata are crucial. The quality of text-image pairs significantly impacts the model's ability to generate images from prompts.

6. Ethical Considerations: Care must be taken to ensure that the fine-tuning dataset does not introduce or amplify biases present in the data. Additionally, copyright and privacy issues should be considered when curating datasets.

Challenges and Best Practices

Fine-tuning diffusion models comes with several challenges, and researchers have developed best practices to address them:

1. Catastrophic Forgetting: Diffusion models can quickly overfit to the fine-tuning dataset, losing their ability to generate diverse images. Techniques like regularization, gradual fine-tuning, and mixing in samples from the original training set can help mitigate this issue.

2. Computational Resources: Fine-tuning large diffusion models can be computationally expensive. Using efficient techniques like LoRA or partial fine-tuning can make the process more accessible.

3. Hyperparameter Tuning: Finding the right learning rate, batch size, and training duration is crucial for successful fine-tuning. Techniques like learning rate warmup and cosine annealing have shown to be effective.

4. Evaluation Metrics: Assessing the quality and diversity of generated images after fine-tuning can be challenging. Using a combination of quantitative metrics (e.g., FID, CLIP score) and human evaluation is often necessary.

5. Prompt Engineering: For text-to-image models, fine-tuning may require adjusting prompt strategies to achieve desired results. Experimenting with different prompt structures and styles can improve generation quality.

6. Regularization: Techniques like dropout, weight decay, and gradient clipping can help prevent overfitting during fine-tuning.

7. Monitoring and Early Stopping: Regularly evaluating the model's performance on a validation set and employing early stopping can prevent overfitting and save computational resources.

8. Iterative Refinement: Fine-tuning is often an iterative process, requiring multiple rounds of training, evaluation, and dataset refinement to achieve desired results.

By carefully considering these factors and employing appropriate techniques, researchers and practitioners can effectively fine-tune diffusion models for a wide range of specialized applications, from generating domain-specific imagery to creating personalized text-to-image systems.

Sampling and Inference

Sampling and inference are crucial aspects of working with diffusion models, as they determine the quality, diversity, and speed of image generation. Various techniques have been developed to improve the sampling process, balancing quality with computational efficiency.

Different Sampling Methods

1. Denoising Diffusion Implicit Models (DDIM): DDIM is a deterministic sampling method that allows for faster sampling compared to the original DDPM approach. It achieves this by defining a non-Markovian forward process that permits skipping steps in the reverse process. DDIM can generate high-quality samples in significantly fewer steps (e.g., 50-100) compared to the thousands required by DDPM.

Key features of DDIM:

• Deterministic sampling path
• Allows for interpolation in latent space
• Supports inversion of real images into the model's latent space

2. DPM-Solver: DPM-Solver is an advanced numerical method specifically designed for fast sampling from diffusion probabilistic models. It formulates the reverse SDE as an ordinary differential equation (ODE) and applies high-order numerical solvers to this ODE.

Advantages of DPM-Solver:

• Can generate high-quality samples in as few as 10-20 steps
• Supports adaptive step size selection for optimal quality-speed trade-off
• Applicable to both discrete-time and continuous-time diffusion models

3. Ancestral Sampling: This is the original sampling method proposed in the DDPM paper. It follows the reverse Markov chain defined by the forward process, sampling noise at each step.

Characteristics:

• Produces diverse samples due to its stochastic nature
• Requires a large number of steps (typically 1000+) for high-quality results
• Simple to implement but computationally expensive

4. PLMS (Pseudo Linear Multistep): PLMS is a sampling method that uses information from previous denoising steps to predict and correct the current step. This approach can reduce the number of required sampling steps while maintaining sample quality.

Benefits:

• Faster than ancestral sampling
• Can produce high-quality samples in 20-50 steps
• Balances speed and sample diversity

Guidance Techniques

Guidance techniques allow for more controlled generation by steering the sampling process towards desired outcomes. These methods have significantly improved the quality and relevance of generated images, especially in text-to-image synthesis.

1. Classifier-Free Guidance: This technique doesn't require an external classifier, making it more efficient and easier to implement. It involves training the diffusion model with both conditional and unconditional samples, then interpolating between these during sampling.

How it works:

• During training, randomly drop the conditioning information for some samples
• During sampling, compute both conditional and unconditional predictions
• Interpolate between these predictions using a guidance scale

Benefits:

• Improves image-text alignment without additional models
• Allows for control over the strength of conditioning
• Can be applied to various types of conditioning (text, class labels, etc.)

2. Classifier Guidance: This method uses an external classifier to guide the sampling process. The classifier's gradients are used to steer the denoising process towards images that better match the desired class or condition.

Characteristics:

• Can provide strong guidance, especially for class-conditional generation
• Requires training and maintaining an additional classifier model
• May introduce biases present in the classifier

3. CLIP Guidance: Leveraging the CLIP (Contrastive Language-Image Pre-training) model, this technique guides the sampling process to better align generated images with text prompts.

How it works:

• Use CLIP to measure the alignment between the current sample and the text prompt
• Adjust the sampling process to maximize this alignment

Advantages:

• Improves text-image alignment without fine-tuning the diffusion model
• Can work with a wide range of text prompts due to CLIP's broad knowledge

Speed-Quality Trade-offs

Balancing generation speed with output quality is a key consideration in practical applications of diffusion models. Several approaches have been developed to optimize this trade-off:

1. Reduced Step Sampling: Using advanced sampling methods like DDIM or DPM-Solver to reduce the number of denoising steps.

Considerations:

• Fewer steps generally lead to faster generation but may reduce sample quality
• The optimal number of steps can vary depending on the specific model and application

2. Progressive Distillation: This technique involves training smaller, faster models to mimic the behavior of larger, slower models at specific stages of the denoising process.

Benefits:

• Can significantly reduce the number of required sampling steps
• Maintains much of the quality of the original model

3. Latent Space Diffusion: Operating in a compressed latent space (as in Latent Diffusion Models) can significantly speed up both training and inference.

Advantages:

• Reduces computational requirements without sacrificing much perceptual quality
• Allows for faster iteration in applications like text-to-image generation

4. Adaptive Sampling: Dynamically adjusting the number of sampling steps or the solver parameters based on the current image content or generation task.

How it works:

• Use heuristics or learned models to determine when additional denoising steps are necessary
• Allocate more computational resources to challenging regions or tasks

5. Hardware Acceleration: Leveraging specialized hardware (e.g., GPUs, TPUs) and optimized implementations can significantly speed up the sampling process.

Techniques:

• Batched generation to maximize hardware utilization
• Mixed-precision arithmetic to balance speed and accuracy
• Kernel fusion to reduce memory bandwidth requirements

The choice of sampling method, guidance technique, and speed optimization approach depends on the specific application requirements, available computational resources, and desired balance between generation speed and output quality. Researchers and practitioners continue to explore novel methods to push the boundaries of what's possible with diffusion models, striving for faster, higher-quality, and more controllable image generation.

Advantages and Limitations

Diffusion models have rapidly gained prominence in the field of generative AI, offering several distinct advantages while also facing certain limitations. Understanding these strengths and weaknesses is crucial for researchers and practitioners working with these models.

High-Quality Outputs

One of the most significant advantages of diffusion models is their ability to generate high-quality, diverse outputs.

Strengths:

1. Photorealistic Details: Diffusion models excel at capturing fine textures and intricate details in generated images. This makes them particularly effective for tasks requiring high fidelity, such as photorealistic image synthesis.

2. Coherent Global Structure: Unlike some other generative models that may struggle with long-range dependencies, diffusion models can maintain coherent global structures in generated images. This is especially evident in their ability to generate complex scenes with multiple interacting elements.

3. Diverse Outputs: Diffusion models exhibit strong mode-covering behavior, meaning they can generate a wide variety of samples that cover different modes of the data distribution. This diversity is crucial for many applications, from data augmentation to creative tools.

4. Stability Across Resolutions: Many diffusion models, especially those using hierarchical approaches or operating in latent spaces, can generate high-quality images across a range of resolutions without requiring separate models for each resolution.

Limitations:

1. Computational Intensity: Generating high-quality outputs often requires a large number of denoising steps, which can be computationally expensive and time-consuming.

2. Quality-Speed Trade-off: While faster sampling methods exist, there's often a trade-off between generation speed and output quality. Achieving both high quality and fast generation remains a challenge.

Flexibility and Controllability

Diffusion models offer remarkable flexibility in terms of the types of data they can model and the level of control they provide over the generation process.

Advantages:

1. Multi-Modal Conditioning: Diffusion models can be conditioned on various types of information, from text and class labels to images and audio. This versatility enables a wide range of applications, from text-to-image synthesis to audio-guided video generation.

2. Fine-Grained Control: Through techniques like classifier-free guidance and attention-based conditioning, diffusion models allow for precise control over generated content. Users can guide the generation process at a detailed level, specifying attributes, styles, and compositions.

3. Adaptability to Different Domains: Diffusion models have shown success across diverse domains, including images, audio, video, and even 3D data. This adaptability makes them valuable for a wide range of research and practical applications.

4. Inpainting and Editing Capabilities: The denoising process of diffusion models naturally lends itself to tasks like inpainting and image editing. These models can seamlessly blend generated content with existing images, maintaining coherence and style.

Limitations:

1. Complexity of Control Mechanisms: While diffusion models offer fine-grained control, effectively leveraging this control can be complex. Crafting precise prompts or conditioning signals often requires expertise and experimentation.

2. Latency in Interactive Applications: The iterative nature of the diffusion process can introduce latency in interactive applications. Real-time editing or generation can be challenging, especially for high-resolution outputs.

3. Unpredictability in Fine Details: While the overall structure and composition can be controlled, the exact fine details of generated images may still have an element of unpredictability, which can be a limitation in some applications requiring precise replication.

Computational Requirements

The computational demands of diffusion models are a significant consideration in their deployment and use.

Advantages:

1. Parallelizable Architecture: The U-Net architecture commonly used in diffusion models is highly parallelizable, allowing for efficient utilization of modern GPU hardware.

2. Scalability: Diffusion models have shown impressive scaling properties, with larger models and more training data generally leading to better results. This scalability suggests potential for continued improvement as computational resources grow.

Limitations:

1. High Training Costs: Training large-scale diffusion models requires substantial computational resources, often necessitating distributed training across multiple GPUs or TPUs. This can make developing new models prohibitively expensive for many researchers and organizations.

2. Inference Time: The iterative denoising process can lead to long inference times, especially for high-quality outputs. This can be a bottleneck in real-time or high-throughput applications.

3. Memory Requirements: Both training and inference can have high memory demands, particularly for high-resolution images or when using large batch sizes. This can limit the size of models that can be run on consumer-grade hardware.

Training Stability

Diffusion models generally offer good training stability compared to some other generative models, but they still face some challenges.

Advantages:

1. Consistent Training Dynamics: Unlike GANs, which can suffer from training instabilities and mode collapse, diffusion models typically exhibit more stable and predictable training behavior.

2. Objective Function Clarity: The well-defined objective function of diffusion models (typically based on denoising score matching) provides a clear optimization target, contributing to training stability.

Limitations:

1. Long Training Times: The need to model the entire denoising trajectory can lead to long training times, even with stable optimization.

2. Sensitivity to Noise Schedule: The choice of noise schedule can significantly impact model performance, and finding the optimal schedule may require extensive experimentation.

3. Challenges in Multi-Modal Data: When training on diverse datasets or with multiple conditioning modalities, balancing the learning of different aspects of the data can be challenging.

Future Directions

The field of diffusion models is rapidly evolving, with ongoing research addressing current limitations and exploring new applications. Several promising directions are emerging:

Ongoing Research Areas

1. Efficiency Improvements:

   • Developing faster sampling methods to reduce the number of required denoising steps.
   • Exploring model compression techniques to reduce the computational and memory requirements of diffusion models.
   • Investigating adaptive sampling strategies that allocate computational resources based on the complexity of the generation task.

2. Multi-Modal Generation:

   • Extending diffusion models to handle multiple modalities simultaneously, such as generating coherent image-text pairs or audio-visual content.
   • Developing models that can seamlessly translate between different modalities (e.g., text to image to video).

3. 3D and Video Generation:

   • Adapting diffusion models for high-quality 3D content generation, including meshes, point clouds, and volumetric data.
   • Improving video generation capabilities, focusing on temporal consistency and long-range dependencies.

4. Controllable Generation:

   • Developing more intuitive and powerful control mechanisms for guiding the generation process.
   • Exploring methods for disentangled representation learning within the diffusion framework to enable fine-grained attribute manipulation.

5. Theoretical Understanding:

   • Deepening the theoretical foundations of diffusion models, including connections to other generative frameworks and optimization theory.
   • Investigating the relationship between model architecture, training dynamics, and generation quality.

Potential Improvements and Extensions

1. Hybrid Architectures:

   • Combining diffusion models with other generative approaches (e.g., autoregressive models, flow-based models) to leverage the strengths of different frameworks.
   • Exploring the integration of diffusion processes into larger, multi-component AI systems.

2. Adaptive Noise Schedules:

   • Developing methods for learning optimal noise schedules dynamically during training or inference.
   • Investigating content-aware noise schedules that adapt to the complexity of different regions in the generated data.

3. Interpretability and Explainability:

   • Developing tools and techniques to better understand and visualize the internal representations and decision-making processes of diffusion models.
   • Exploring methods to make the generation process more transparent and controllable.

4. Ethical AI and Bias Mitigation:

   • Investigating techniques to detect and mitigate biases in diffusion models.
   • Developing frameworks for responsible development and deployment of diffusion-based generative AI systems.

5. Domain-Specific Optimizations:

   • Tailoring diffusion models for specific domains or applications, such as medical imaging, scientific visualization, or industrial design.
   • Exploring domain-specific architectures and training strategies to improve performance in targeted areas.

6. Continual Learning and Adaptation:

   • Developing methods for efficiently updating diffusion models with new data or concepts without full retraining.
   • Exploring few-shot and zero-shot learning capabilities within the diffusion framework.

7. Robustness and Reliability:

   • Improving the robustness of diffusion models to adversarial attacks and out-of-distribution inputs.
   • Developing uncertainty quantification methods for diffusion-based generation to provide reliability estimates for generated content.

Conclusion

Diffusion models have emerged as a powerful and versatile class of generative AI models, significantly impacting various fields from computer vision to content creation. Let's recap the key points and consider their broader impact:

Recap of Key Points

1. Versatility: Diffusion models have demonstrated exceptional capabilities across a wide range of tasks, including image generation, text-to-image synthesis, inpainting, and editing.

2. High-Quality Outputs: These models excel at producing detailed, coherent, and diverse outputs, often surpassing other generative approaches in terms of visual quality.

3. Controllability: Through various conditioning and guidance techniques, diffusion models offer fine-grained control over the generation process, enabling precise manipulation of generated content.

4. Scalability: Diffusion models have shown impressive scaling properties, with larger models and more data generally leading to better results.

5. Challenges: Despite their strengths, diffusion models face challenges in computational requirements, inference speed, and the complexity of fine-tuning for specific tasks.

6. Active Research: The field is rapidly evolving, with ongoing work addressing current limitations and exploring new applications across multiple modalities and domains.

Impact on AI and Creative Fields

The rise of diffusion models has had a profound impact on both AI research and creative industries:

1. Democratization of Content Creation: Tools based on diffusion models, such as Stable Diffusion and DALL-E, have made advanced image generation capabilities accessible to a wide audience, empowering artists, designers, and content creators.

2. New Paradigms in AI Research: Diffusion models have introduced novel concepts and techniques to the field of generative AI, spurring new lines of research and cross-pollination with other areas of machine learning.

3. Ethical Considerations: The ability to generate highly realistic content has raised important ethical questions and challenges regarding misinformation, copyright, and the potential misuse of these technologies.

4. Industry Applications: From advertising and entertainment to product design and scientific visualization, diffusion models are finding applications across various industries, potentially transforming workflows and creative processes.

5. Interdisciplinary Collaboration: The development and application of diffusion models are fostering collaboration between AI researchers, artists, ethicists, and domain experts across different fields.

6. Pushing the Boundaries of AI Capabilities: The success of diffusion models in generating complex, coherent content is expanding our understanding of what's possible with AI, potentially paving the way for more advanced forms of machine creativity and understanding.

In conclusion, diffusion models represent a significant leap forward in generative AI, offering unprecedented quality, control, and versatility. As research continues to address current limitations and explore new frontiers, these models are likely to play an increasingly important role in shaping the future of AI and its applications across various domains. The ongoing development of diffusion models not only pushes the boundaries of technical capabilities but also prompts important discussions about the role of AI in creative processes, the nature of authorship, and the ethical implications of powerful generative technologies.