Evaluating Classification Models: Confusion Matrices and ROC Curves

Confusion Matrix

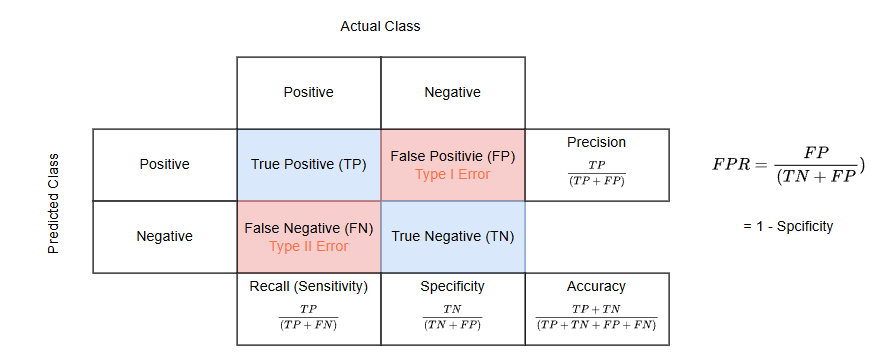
Structure and Components

A confusion matrix is typically presented as a table with four key components:

1. True Positives (TP): Cases where the model correctly predicts the positive class.
2. True Negatives (TN): Cases where the model correctly predicts the negative class.
3. False Positives (FP): Cases where the model incorrectly predicts the positive class (Type I error).
4. False Negatives (FN): Cases where the model incorrectly predicts the negative class (Type II error).

For binary classification problems, the matrix is typically a 2x2 grid. However, it can be expanded for multi-class classification problems, where each row represents the actual class and each column represents the predicted class.

Type I Error Examples

A Type I error occurs when we reject a true null hypothesis, resulting in a false positive.

1. Medical Diagnosis: A doctor diagnoses a patient with cancer based on test results, but the patient actually doesn't have cancer. This false positive diagnosis may lead to unnecessary treatments, anxiety, and financial burden.

2. Quality Control: A manufacturing plant rejects a batch of products believing they are defective when they actually meet quality standards. This could result in wasted resources and unnecessary production costs.

3. Criminal Justice: An innocent person is convicted of a crime they didn't commit based on circumstantial evidence. This false conviction can lead to wrongful imprisonment and severe personal consequences.

4. Drug Testing: An athlete tests positive for a performance-enhancing drug due to a false positive result, leading to disqualification or suspension when they haven't actually used any banned substances.

Type II Error Examples

A Type II error occurs when we fail to reject a false null hypothesis, resulting in a false negative.

1. Medical Screening: A cancer screening test fails to detect cancer in a patient who actually has the disease. This false negative could delay crucial treatment and worsen the patient's prognosis.

2. Product Safety: A company's quality control process fails to detect a defect in a product, allowing unsafe items to reach consumers. This could lead to injuries, product recalls, and damage to the company's reputation.

3. Environmental Protection: A test designed to detect water pollution fails to identify contamination in a water source. This could result in people consuming unsafe water and potential health hazards.

4. Financial Fraud Detection: A bank's fraud detection system fails to flag a series of suspicious transactions that are actually fraudulent. This could lead to significant financial losses for the bank and its customers.

5. Drug Efficacy Studies: A clinical trial concludes that a new drug is not effective in treating a disease when it actually is. This Type II error could prevent a potentially life-saving medication from reaching patients who need it.

Key Metrics Derived from Confusion Matrix

The confusion matrix allows us to calculate several important performance metrics:

Accuracy: The proportion of correct predictions (both true positives and true negatives) among the total number of cases examined.

Precision: The proportion of correct positive predictions out of all positive predictions.

Recall (Sensitivity): The proportion of actual positive cases that were correctly identified.

Specificity: The proportion of actual negative cases that were correctly identified.

F1-Score: The harmonic mean of precision and recall, providing a single score that balances both metrics.

Benefits and Applications

Confusion matrices offer several advantages:

1. They provide a detailed breakdown of correct and incorrect classifications for each class.
2. They help identify which classes are being confused with each other.
3. They are particularly useful for imbalanced datasets where accuracy alone may be misleading.

Interpreting a Confusion Matrix

To interpret a confusion matrix:

1. Look at the diagonal elements, which represent correct classifications.
2. Examine off-diagonal elements to see where misclassifications occur.
3. Calculate performance metrics to get a comprehensive view of model performance.

ROC curve

The ROC (Receiver Operating Characteristic) curve is a powerful tool for evaluating the performance of binary classification models. It complements the confusion matrix by providing a visual representation of the trade-off between true positive rate and false positive rate across various classification thresholds.

Key Components of ROC Curve

1. True Positive Rate (TPR): Also known as sensitivity or recall, TPR is plotted on the y-axis. It's calculated as:

   $TPR = \frac{True Positives}{True Positives + False Negatives}$

2. False Positive Rate (FPR): Plotted on the x-axis, FPR is calculated as:

   $FPR = \frac{False Positives}{False Positives + True Negatives}$

Interpreting the ROC Curve

• The curve plots TPR against FPR at various threshold settings.
• A perfect classifier would have a point in the upper left corner (0,1), representing 100% sensitivity and 100% specificity.
• The diagonal line from (0,0) to (1,1) represents the performance of a random classifier.
• Curves closer to the top-left corner indicate better-performing models.

Area Under the Curve (AUC)

The AUC is a single scalar value that quantifies the overall performance of the classifier:

• AUC ranges from 0 to 1, with higher values indicating better performance.
• An AUC of 0.5 suggests no discrimination (equivalent to random guessing).
• AUC values can be interpreted as follows:
  • 0.9 - 1.0: Excellent
  • 0.8 - 0.9: Good
  • 0.7 - 0.8: Fair
  • 0.6 - 0.7: Poor
  • 0.5 - 0.6: Fail

Advantages of ROC Curves

1. They provide a comprehensive view of classifier performance across all possible thresholds.
2. ROC curves are insensitive to class imbalance, making them useful for evaluating models on imbalanced datasets.
3. They allow for easy comparison between different classification models.

Limitations and Considerations

• ROC curves may not be ideal for highly imbalanced datasets, where precision-recall curves might be more informative.
• They don't provide information about the actual predicted probabilities, only their rank ordering.

Practical Application

In Python, you can easily plot ROC curves using libraries like scikit-learn and matplotlib. Here's a basic example:

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt

# Assuming y_true are the true labels and y_scores are the predicted probabilities
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)

plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (AUC = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()

By using ROC curves in conjunction with confusion matrices, you can gain a comprehensive understanding of your classification model's performance and make informed decisions about threshold selection and model comparison.